What is the highest power of 7 that divides 50!?

This question is from the topic Number Theory. It is a question on factorials and is about finding the highest power of a prime factor that will divide the factorial.

Question

What is the highest power of 7 that can divide 5000! without leaving a remainder? (5000! means factorial 5000)

1. 4998
2. 714
3. 832
4. 816

Correct Answer - 832. Choice (3)

Explanatory Answer

5000! = 5000 * 4999 * 4998 * 4997 * ............ 1.
Between 1 and 5000, there are numbers which will be divisible by 7, 7², 7³ and 7⁴.

There are = 714 numbers that are exactly divisible by 7 between 1 and 5000.

So there are 714 Sevens contained in these numbers.

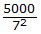
There are = 102 numbers that are exactly divisible by 49 between 1 and 5000.

These numbers are also a part of the 714 numbers. But we add it again because they are divisible by 7² and hence to account for the second 7 in these numbers.

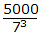
There are = 14 numbers that are divisible by 343 (i.e., 7³) between 1 and 5000.

These numbers will be a part of the previous set 714 and 102 - however, we add these 14 numbers to account for the third seven in these numbers as these numbers are multiples of 343 or 7³.

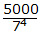
And finally, there are = 2 numbers that are divisible by 2401 (i.e. 7⁴).

Therefore, there will be a total of 714 + 102 + 14 + 2 = 832 sevens contained in 5000!
Hence the highest power of 7 that can divide 5000! without leaving a remainder is 832.

Correct answer choice (3)

Level of difficulty : Moderate to Difficult

---

More Questions Answers on Number Theory

CAT, XAT, TANCET Practice Questions and Answers : Listed Topicwise

Number Theory		Permutation Combination		Probability		Inequalities
Geometry		Mensuration		Trigonometry		Coordinate Geometry
Percentages		Profit Loss		Ratio Proportion		Mixtures Alligation
Speed Time Distance		Pipes Cisterns		Interest		Races
Average, Mean		AP, GP, HP		Set Theory		Clocks Calendars
Algebra		Function		English Grammar		General Awareness
Data sufficiency		TANCET Papers		XAT Papers