Mensuration, Solid Geometry Questions

A collection of questions that typically appear in the TANCET, CAT, GMAT, GRE, and SAT from the topic Mensuration and solid geometry. These questions will guide you through your TANCET, GMAT, CAT and other MBA entrance test preparation. Concepts covered include area, perimeter circumference of squares, rectangles, other quadrilaterals and area and circumference of circles and semicircles. Also includes surface area and volume of solids such as cubes, cuboids (rectangular cubes), cylinders, cones, spheres and hemispheres.

1. A 5 cubic centimeter cube is painted on all its side. If it is sliced into 1 cubic centimer cubes, how many 1 cubic centimeter cubes will have exactly one of their sides painted?

   1. 9
   2. 61
   3. 98
   4. 54

   Concept: Cubes and surfaces

   Choice (4)54 1 cc cubes will have exactly one of their sides painted Correct answer Explanatory Answer Medium

2. The area of a square field is 24200 sq m. How long will a lady take to cross the field diagonally at the rate of 6.6 km/hr?

   1. 3 minutes
   2. 2 minutes
   3. 2.4 minutes
   4. 2 minutes 40 seconds

   Concept: Area of Squares

   Choice (2)2 minutes Correct answer Explanatory Answer Easy

3. The circumference of the front wheel of a cart is 30 ft long and that of the back wheel is 36 ft long. What is the distance travelled by the cart, when the front wheel has done five more revolutions than the rear wheel?

   1. 20 ft
   2. 25 ft
   3. 750 ft
   4. 900 ft

   Concept: Circumference of circles

   Choice (4)900 ft Correct answer Explanatory Answer Hard

4. If the sides of a triangle measure 72, 75 and 21, what is the measure of its in radius?

   1. 37.5
   2. 24
   3. 9
   4. 15

   Concept: Right Triangles

   Choice (3)The in radius measures 9 units Correct answer Explanatory Answer Medium

5. A 5 cm cube is cut into as many 1 cm cubes as possible. What is the ratio of the surface area of the larger cube to that of the sum of the surface areas of the smaller cubes?

   1. 1 : 6
   2. 1 : 5
   3. 1 : 25
   4. 1 : 125

   Concept: Surface area of cubes

   Choice (2)1 : 5 Correct answer Explanatory Answer Medium

6. If each interior angle of a regular polygon is 150 degrees, then it is a/an ______________

   1. Octagon
   2. Decagon
   3. Dodecagon
   4. Tetrahedron

   Concept: Regular Polygon

   Choice (3)Dodecagon Correct answer Explanatory Answer Easy

7. Four horses are tethered at 4 corners of a square field of side 70 metres so that they can just about reach one another. The area left ungrazed by the horses is:

   1. 1050 sq.m
   2. 3850 sq.m
   3. 950 sq.m
   4. 1075 sq.m

   Concept: Squares and sectors

   Choice (1)1050 sq.m area will be left ungrazed by the horses Correct answer Explanatory Answer Medium

8. A square sheet of paper is converted into a cylinder by rolling it along its length. What is the ratio of the base radius to the side of the square?

   1. \\frac{1}{2π}\\)
   2. \\frac{(\sqrt2)}{π}\\)
   3. \\frac{1}{(\sqrt2π)}\\)
   4. \\frac{1}{π}\\)

   Concept: Cylinders

   Choice (1){1/(2π)} Correct answer Explanatory Answer Easy

9. The surface area of the three coterminous faces of a cuboid are 6, 15, 10 sq.cm respectively. Find the volume of the cuboid.

   1. 30 cc
   2. 20 cc
   3. 40 cc
   4. 35 cc

   Concept: Volume of cuboids

   Choice (1)The volume of the cuboid is 30 cc Correct answer Explanatory Answer Medium

10. If the diagonal and the area of a rectangle are 25 m and 168 m², what is the length of the rectangle?

    1. 17 m
    2. 31 m
    3. 12 m
    4. 24 m

    Concept: Rectangle

    Choice (4)The length of the rectangle is 24 m Correct answer Explanatory Answer Easy

11. A 4 cm cube is cut into 1 cm cubes. What is the percentage increase in the surface area after cutting?

    1. 4%
    2. 300%
    3. 75%
    4. 400%

    Concept: Surface area of cubes

    Choice (2)The surface area increased by 300% Correct answer Explanatory Answer Medium

12. A regular hexagon is inscribed in a circle of radius r cm. What is the perimeter of the regular hexagon?

    1. 3r
    2. 6r
    3. \\sqrt{72}r\\)
    4. 9r

    Concept: Regular Hexagon

    Choice (2)The perimeter of the hexagon is 6r cm Correct answer Explanatory Answer Easy

13. If x units are added to the length of the radius of a circle, what is the number of units by which the circumference of the circle is increased?

    1. x
    2. 2
    3. 2π
    4. 2πx
    5. x²

    Concept: Circles circumference

    Choice (4)The circumference will increase by 2πx Correct answer Explanatory Answer Easy TANCET 2008

14. ABCD has area equal to 28. BC is parallel to AD. BA is perpendicular to AD. If BC is 6 and AD is 8, then what is CD?

    

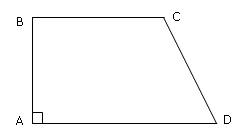
    1. 2√2
    2. 2√3
    3. 4
    4. 2√5
    5. 6

    Concept: Trapezium, right triangles

    Choice (4)The length of CD is 2√5 Correct answer Explanatory Answer Easy TANCET 2008

15. Which of the following figures has the largest area?

    1. A circle of radius √2
    2. An equilateral triangle whose sides each have length 4
    3. A triangle whose sides have lengths 3, 4 and 5
    
    
    1. I
    2. II
    3. III
    4. I and III
    5. II and III

    Concept: Area comparison

    Choice (2)II Correct answer Explanatory Answer Easy TANCET 2008

16. The hexagon ABCDEF is regular. That means all its sides are of the same length and all its interior angles are of the same size. Each side of the hexagon is 2 m. What is the area of the rectangle BCEF?

    

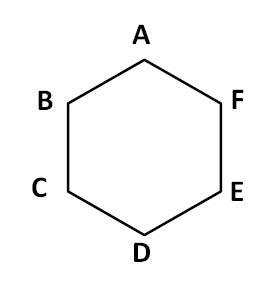
    1. 4 sq.m
    2. 4√3 sq.m
    3. 8 sq.m
    4. 4 + 4√3 sq.m
    5. 12 sq.m

    Concept: Regular Hexagons

    Choice (2)4√3 sq.m Correct answer Explanatory Answer Easy TANCET 2008

17. Ram a farmer, managed to grow shaped-watermelons inside glass cases of different shapes. The shapes he used were: a perfect cube, hemi-spherical, cuboid, cylindrical along with the normal spherical shaped watermelons. Thickness of the skin was same for all the shapes. Each of the glass cases was so designed that the total volume and the weight of the all the water-melons would be equal irrespective of the shape.
    
    A customer wants to buy water-melon for making juice, for which the skin of the water-melon has to be peeled off, and therefore is a waste. Which shape should the customer buy?
    

    1. Cube
    2. Hemi-sphere
    3. Cuboid
    4. Cylinder
    5. Normal spherical

    Concept: Solids - surface area

    Choice (E)Normal spherical Correct answer Explanatory Answer Medium XAT 2012

18. The figure below has been obtained by folding a rectangle. The total area of the figure (as visible) is 144 square meters. Had the rectangle not been folded, the current overlapping part would have been a square. What would have been the total area of the original unfolded rectangle?

    

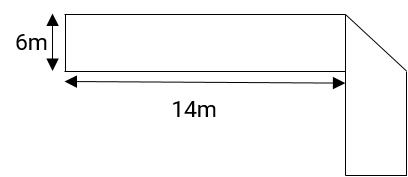
    1. 128 square meters
    2. 154 square meters
    3. 162 square meters
    4. 172 square meters
    5. None of the above

    Choice CThe area of the unfolded rectangle is 162 sq m Correct answer Explanatory Answer Video Explanation XAT 2015

19. A solid metal cylinder of 10 cm height and 14 cm diameter is melted and re-cast into two cones in the proportion of 3 : 4 (volume), keeping the height 10 cm. What would be the percentage change in the flat surface area before and after?

    1. 9%
    2. 16%
    3. 25%
    4. 50%
    5. None of the above

    Choice DThe flat surace area increases by 50% Correct answer Explanatory Answer Video Explanation XAT 2015

20. A circular road is constructed outside a square field. The perimeter of the square field is 200 ft. If the width of the road is 7√2 ft. and cost of construction is Rs. 100 per sq. ft. Find the lowest possible cost to construct 50% of the total road.

    1. Rs.70,400
    2. Rs.1,25,400
    3. Rs.1,40,800
    4. Rs.2,35,400
    5. None of the above

    Choice BThe lowest cost of constructing 50% of the road is Rs.1,25,400 Correct answer Explanatory Answer Video Explanation XAT 2015