XAT 2014 Quant : AP & Divisibility
Question
2. Properties of odd and even numbers 2 concepts
x, 17, 3x - y2 - 2 and 3x + y2 - 30 are four consecutive terms of an increasing arithmetic sequence. The sum of the four numbers is divisible by:
- 2
- 3
- 5
- 7
- 11
Correct Answer Choice A. The sum is divisible by 2.
Explanatory Answer
-
Step by step solution
The question does NOT state that the terms are all integers. That is an unstated assumption and is essential to solve the question.
- The four terms are in an arithmetic sequence and the sequence is an ascending sequence. i.e., the second term is greater than the first term and so on.
- The sum of the four terms = x + 17 + 3x - y2 - 2 + 3x + y2 - 30 = 7x - 15
- If we get an idea about the type of number x is, we will be able find the answer to the question.
- Because these 4 terms are in an arithmetic sequence, the difference between any two terms will be the same.
So, 17 - x = (3x + y2 - 30) - (3x - y2 - 2)
i.e., 17 - x = 2y2 - 28
Or 45 - x = 2y2 - Because y is an integer, 2y2 has to be an even integer.
Properties of Odd and Even numbers1. Difference between two odd numbers is even
2. Difference between an odd and an even number is oddUnless x is odd, 45 - x cannot be even.
So, we can deduce that x is odd. - The sum of the four terms is 7x - 15
x is odd; Properties of Odd and Even numbersProduct of two odd numbers is odd.So, 7x will also be odd.
Hence, Properties of Odd and Even numbersDifference between two odd numbers is even.7x - 15 will be even.
Therefore, the sum of the 4 terms will be divisible by 2.
The correct answer is Choice A.
- The four terms are in an arithmetic sequence and the sequence is an ascending sequence. i.e., the second term is greater than the first term and so on.
-
Alternative Method
Of the 4 terms in AP, the second term is 17, which is an odd number.
The common difference has to be either odd or even
Sum of an odd number and an even number is odd and the sum of two odd numbers is evenPossibility 1: If the common difference is odd, the first term will be even, the third term will be even and the fourth term will be odd.
i.e., two of the terms of the sequence are odd and two are even.
Sum of two odd numbers and two even numbers is even.Possibility 2: If the common difference is even, all four terms will be odd.
Sum of 4 odd numbers is even.So, irrespective of whether the common difference is odd or even, the sum of the four terms is even.
Hence, the sum will be divisible by 2
-
Formulae to remember in Arithmetic Sequence
An arithmetic progression is such a sequence in which every subsequent term of the sequence is obtained by adding the preceding term with a constant number. This constant number is called the common difference(d) of the sequence.
e.g., 2, 4, 6, 8, 10 is an arithmetic sequence.
The second term is obtained by adding the first term by 2. The third term is obtained by adding the second term by 2 and so on.Formula 1: nth term of a Arithmetic Progression an = a1 + (n - 1)d, where a is the first term of the sequence and d is the common difference.
Formula 2: Sum of the first n terms of a arithmetic progression =
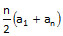
Alternatively, you can find the sum using this formula Sn =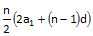
More Questions on Arithmetic, Geometric Progression
- Find the sum of terms of a GP
- AP: find a term; sum known
- Sum of AP having -ve common difference
- AP: find a terms; sum & product given
- Sum of an AP Series
- CAT 2003: Find sum of terms of an AP
- AP: Integers divisible by 4 or 9
- TANCET 2013: Sum of a GP
- XAT 2014: AP & Divisibility
- XAT 2015: Sum of an AP
- Logarithm terms in an AP
- Speed Distance Time & AP
Online TANCET MBA Course
Try it Free!
Register in 2 easy steps and start learning in 5 minutes!
Already have an Account?
XAT TANCET Practice Questions - Listed Topic wise
- Number Theory
- Permutation Combination
- Probability
- Inequalities
- Geometry
- Coordinate Geometry
- Mensuration
- Trigonometry
- Data Sufficiency
- Percentages
- Profit Loss
- Ratio Proportion
- Mixtures & Alligation
- Speed Distance & Time
- Pipes, Cisterns & Work, Time
- Simple & Compound Interest
- Races
- Averages & Statistics
- Progressions : AP, GP & HP
- Set Theory
- Clocks Calendars
- Linear & Quadratic Equations
- Functions
- English Grammar
- General Awareness
