AP and Speed Distance Time Problem

This quant practice question covers basics of speed distance time and uses concepts of arithmetic progression as the two travellers travel at speeds which are in an arithmetic progression. Try and solve this question carefully as there are a couple of places where one could make mistakes in this question.

Question

Medium Quant

Two travelers set out on a long odyssey. The first traveler starts from city X and travels north on a certain day and covers 1 km on the first day and on subsequent days, he travels 2 km more than the previous day. After 3 days, a second traveler sets out from city X in the same direction as the first traveler and on his first day he travels 12 km and on subsequent days he travels 1 km more than the previous day. On how many days will the second traveler be ahead of the first?

2 days
6 days
From the 2nd day after the 2nd traveler starts
From the 3rd day after the 2nd traveler starts

Correct Answer Choice (2). The second traveler is ahead of the first for 6 days.

Explanatory Answer

Step 1 Step 2 Step 3 Tabs

Travel Pattern of Traveller 2

Day 1: 1 km; Day 2: (1 + 2) = 3 km; Day 3: (1 + 2 + 2) = 5km and so on
i.e. on each of these days he covers the following distance Day 1: 1km, Day 2: 3km, Day 3: 5km and so on.

The distances covered each day by the first traveller is in an AP with the first term being 1 and the common difference being 2

After 3 days, the first traveler would have traveled 9 kms. He is ahead of the second traveler at the end of 3 days by 9 kms.

Travel Pattern of Traveller 2

The second traveler travels as follows: On his first day he travels 12 kms, his second day he travels 13 kms and so on.

The distances covered each day by the second traveller is in an AP with the first term being 12 and the common difference being 1
Compute total distance covered by each of the travellers

Let the number of days travelled by the second traveller be n.
Therefore, the first traveller would have travelled for (n + 3) days.
Traveler 1 has covered a total distance of 1+ 3 + 5 + 7 + ..... + (n + 3) km.

The total distance covered by traveler 1 is the summation of the AP.

Sum of an AP =

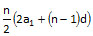
Total distance travelled by traveller 1 in (n + 3) days = \\frac{n + 3} {2} [{2({1}) + ({n + 3 - 1}) (2)}] \\)

The above term simplifies as (n + 3)²

The total distance covered by the second traveler = 12 + 13 + 14 + ... + n terms

Total distance travelled by traveller 2 in n days = \\frac{n} {2} [{2({12}) + ({n - 1}) (1)}] \\) = \\frac{n(n + 23)} {2} \\)
Compute the number of days traveller 2 was ahead

On the days that the second traveller is ahead of the first one, the total distance covered by the second traveller till that day will be more than the total distance covered by the first traveller.

Note: All values calculated are with respect to the day from which the second traveller started travelling

Therefore, let us solve the inequality \\frac{n(n + 23)} {2} \\) > (n + 3)²

n² + 23n > 2(n² + 6n + 9)
Or n² - 11n + 18 < 0

The quadratic factorizes as (n - 2)(n - 9) < 0

Possibility 1: (n - 2) > 0 AND (n - 9) < 0
i.e., n > 2 AND n < 9
Therefore, 2 < n < 9

Possibility 2: (n - 2) < 0 AND (n - 9) > 0
i.e., n < 2 AND n > 9
Infeasible solution

Therefore, starting the 3rd day and up to the 8th day the second traveller was ahead of the first traveller

The correct answer is Choice (2). 6 days