XAT 2015 Quant & DI: Quadratic Equations
This question appeared as a part of the quantitative reasoning and data interpretation section of the XAT 2015. Question 8 of a total of 33 questions that appeared in this section in XAT 2015. This one is an easy aptitude / quant question that tests concepts about quadratic equations and the curves that these equations represent.
Question
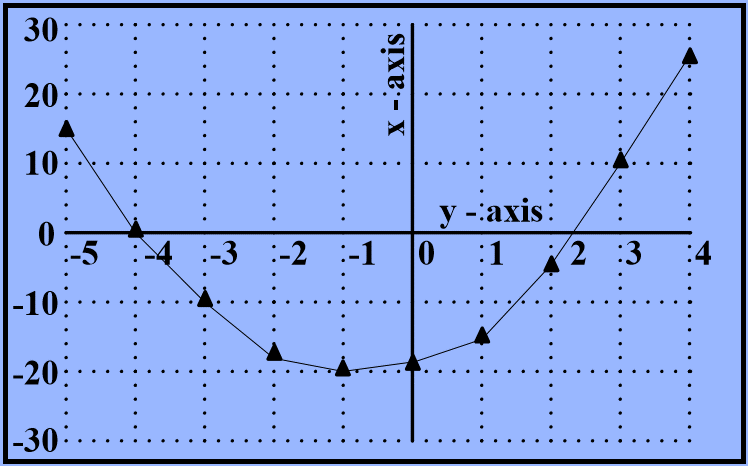
Find the equation of the graph shown below.
- y = 3x - 4
- y = 2x2 - 40
- x = 2y2 - 40
- y = 2x2 + 3x - 19
- x = 2y2 + 3y - 19
Correct Answer Choice E. x = 2y2 + 3y - 19
Explanatory Answer
-
Given Data
In the graph, x and y-axes have been swapped from the conventional ones.
i.e,. horizontal axis has been named y-axis and the vertical axis has been named x-axis.Key Inference
The curve is a parabola.
A parabola will have an equation of the form y = ax2 + bx + c
However, in our case, the x and y axes have been swapped.
So, the equation has to be of the form x = ay2 + by + cPoints of Interest
To determine which of the equations fits the curve given, we are going to substitute values of x or y from the graph in the equations and check for a match. We need two to three points to determine that. Let us select points where at least one of the coordinates is 0. The points of interest therefore are:- When y is around -4, x = 0
- When y is between 2 and 3, x = 0
- When y is 0, x is around -20
What is the approach?
Substitute x = 0 in the choices that match the form of equation stated in the key inference step and see which one matches the data.
Cross check with another value when y = 0.
The choice that matches both conditions is the answer. -
Compute the equation
The equation has to be of the form x = ay2 + by + c.
A quick look at the choices tells us that we can eliminate choices A, B, and D.
Choice A is a linear equation. So, it represents a straight line. Rule it out.
Choices B and D are of the form y = ax2. Our axes are swapped. So, choice B can also be ruled out.Choice C: x = 2y2 – 40
Substitute y = -4 in the equation.
We get x = 2(-4)2 – 40 = 32 – 40 = -8.
However, we know that when y = -4, x = 0.So, Choice C cannot be the answer.
Choice E: x = 2y2 + 3y – 19
When y = -4, x = 2(-4)2 +3(-4) – 19 = 32 – 31 = 1.
So, when y is around -4, it will be 0.Let us validate it with one more data point.
When y = 0, x = 2(0)2 + 3(0) – 19 = -19.
The value of x is around -20 as indicated in the curve.The correct answer is Choice E.
Video Explanation
Online TANCET MBA Course
Try it Free!
Register in 2 easy steps and start learning in 5 minutes!
Already have an Account?
XAT TANCET Practice Questions - Listed Topic wise
- Number Theory
- Permutation Combination
- Probability
- Inequalities
- Geometry
- Coordinate Geometry
- Mensuration
- Trigonometry
- Data Sufficiency
- Percentages
- Profit Loss
- Ratio Proportion
- Mixtures & Alligation
- Speed Distance & Time
- Pipes, Cisterns & Work, Time
- Simple & Compound Interest
- Races
- Averages & Statistics
- Progressions : AP, GP & HP
- Set Theory
- Clocks Calendars
- Linear & Quadratic Equations
- Functions
- English Grammar
- General Awareness
