Quantitative Reasoning : Inequalities

Question

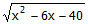
For what values of 'x' is the function defined in the real domain?

1. -10 < x < 4
2. –4 < x < 10
3. x does not lie between the closed interval –10 and 4
4. x does not lie between the open interval –4 and 10
   
   

Correct Answer

Choice (4). x does not lie between the open interval –4 and 10

Explanatory Answers

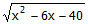
The function is defined in the real domain only when x² – 6x – 40 > 0.

When x² – 6x – 40 is < 0, the function will be imaginary.

Now let us find out the range of values for which x² – 6x – 40 > 0.

Factorizing the quadratic expression, we get (x – 10)(x + 4) > 0

This expression (x – 10)(x + 4) will be greater than or equal to 0 when both (x – 10) and (x + 4) are greater than or equal to 0 or when both (x - 10) and (x + 4) are less than or equal 0.

Case 1:

When both (x – 10) and (x + 4) are greater than or equal to 0.

x > 10 and x > - 4 => when x > 10 it will be greater than –4.

Therefore, it will suffice to say that x > 10

Case 2:

When both (x - 10) and (x + 4) are less than or equal to 0.

i.e. x < 10 and x < -4 => when x < -4, it will less than 10.

Therefore, it will suffice to say that x < -4

Hence, the range in which the given function will be defined in the real domain will be when x does not lie between –4 and 10.

---

More Questions Inequality

CAT, XAT, TANCET Practice Questions and Answers : Listed Topicwise

Number Theory		Permutation Combination		Probability		Inequalities
Geometry		Mensuration		Trigonometry		Coordinate Geometry
Percentages		Profit Loss		Ratio Proportion		Mixtures Alligation
Speed Time Distance		Pipes Cisterns		Interest		Races
Average, Mean		AP, GP, HP		Set Theory		Clocks Calendars
Algebra		Function		English Grammar		General Awareness
Data sufficiency		TANCET Papers		XAT Papers