XAT 2015 Q10 : Area of right triangle
This aptitude question appeared as a part of the quantitative reasoning and data interpretation section of the XAT 2015. Question 10 of a total of 33 questions that appeared in this section in XAT 2015. This one is a medium level difficulty question and tests the following concepts: Similar triangles, trigonometric identities, and area of triangles.
Question
2. Trigonometric Identities
3. Similar triangles 3 concepts
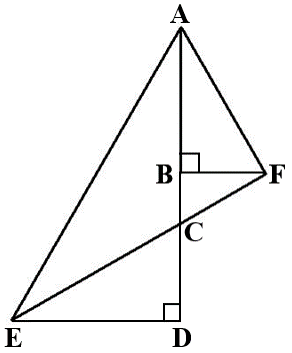
In the diagram below, CD = BF = 10 units and ∠CED = ∠BAF = 30o. What would be the area of triangle AED? (Note: Diagram below may not be drawn to scale.)
- 100 x (\\sqrt{2}\\) + 3)
- \\frac{100}{(\sqrt3 + 4)}\\)
- \\frac{50}{(\sqrt3 + 4)}\\)
- 50 x (\\sqrt{3}\\) + 4)
- None of the above
Correct Answer Choice D. 50 x (\\sqrt{3}\\) + 4)
Explanatory Answer
-
Decode the given data
Given Data:
- CD = BF = 10 units
- ∠CED = ∠BAF = 30o

The triangle AED is a right triangle.
The area of the triangle can be computed if we know the measure of AD and ED, the two perpendicular sides.
1. Compute length of ED
In right triangle CDE
∠CED = 30oTherefore, tan ∠CED = tan 30o = \\frac{1}{\sqrt3}\\) = \\frac{CD}{ED}\\)
Therefore ED = \\sqrt{3}\\) x CD = 10\\sqrt{3}\\)
2. Compute length of AB
In right triangle ABF
∠BAF = 30o
Therefore, tan ∠BAF = tan 30o = \\frac{1}{\sqrt3}\\) = \\frac{BF}{AB}\\)
Hence, AB = \\sqrt{3}\\) x BF = 10\\sqrt{3}\\)3. Compute length of BC
Triangles EDC and FBC are right triangles. ∠EDC = ∠FBC. Both are right angles.
∠DCE = ∠BCF. Vertically opposite angles are equal.Because two angles of the two triangles EDC and FBC are equal these two triangles are similar triangles.
So, ∠BFC = ∠CED = 30o
tan ∠BFC = tan 30o = \\frac{1}{\sqrt3}\\) = \\frac{BC}{BF}\\)
We know BF = 10
So, BC = \\frac{10}{\sqrt3}\\). -
Compute AD (Add 1 + 2 + 3 from step 1)
AD = AB + BC + CD = 10\\sqrt{3}\\) + \\frac{10}{\sqrt3}\\) + 10
Compute Area
Area of triangle AED = \\frac{1}{2}\\) ED×AD = \\frac{1}{2}\\) × 10 \\sqrt{3}\\) × (10 + \\frac{10}{\sqrt3}\\) + 10\\sqrt{3}\\)) = 50 × ( \\sqrt{3}\\) + 4)
The correct answer is Choice D.
Video Explanation
Online TANCET MBA Course
Try it Free!
Register in 2 easy steps and start learning in 5 minutes!
Already have an Account?
XAT TANCET Practice Questions - Listed Topic wise
- Number Theory
- Permutation Combination
- Probability
- Inequalities
- Geometry
- Coordinate Geometry
- Mensuration
- Trigonometry
- Data Sufficiency
- Percentages
- Profit Loss
- Ratio Proportion
- Mixtures & Alligation
- Speed Distance & Time
- Pipes, Cisterns & Work, Time
- Simple & Compound Interest
- Races
- Averages & Statistics
- Progressions : AP, GP & HP
- Set Theory
- Clocks Calendars
- Linear & Quadratic Equations
- Functions
- English Grammar
- General Awareness
