XAT 2015 Quant & DI: Coordinate Geometry Q9

This aptitude practice question appeared in the quantitative reasoning and data interpretation section of the XAT 2015. Question 9 of a total of 33 questions that appeared in this section in XAT 2015. This one is an easy question and tests the concept of finding lengths of line segments given coordinates of two points on the line segment.

Question

Two diagonals of a parallelogram intersect each other at coordinates (17.5, 23.5). Two adjacent points of the parallelogram are (5.5, 7.5) and (13.5, 16). Find the lengths of the diagonals.

1. 15 and 30
2. 15 and 40
3. 17 and 30
4. 17 and 40
5. Multiple solution are possible

  Correct Answer      Choice D. The lengths of the diagonals are 17 and 40.

Explanatory Answer

Given Data

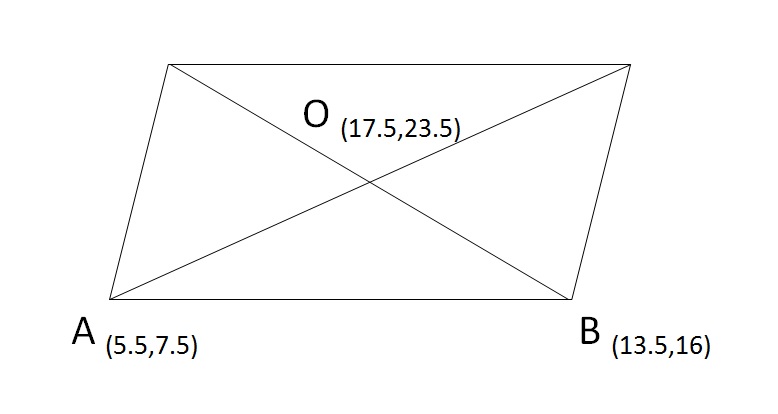
1. Diagonals of the parallelogram intersect at 17.5, 23.5. Let us call this point O (17.5, 23.5).
2. Coordinates of two adjacent points of the parallelogram are (5.5, 7.5) and (13.5, 16)
   Let us say the points are A(5.5, 7.5) and B(13.5, 16)

Key facts

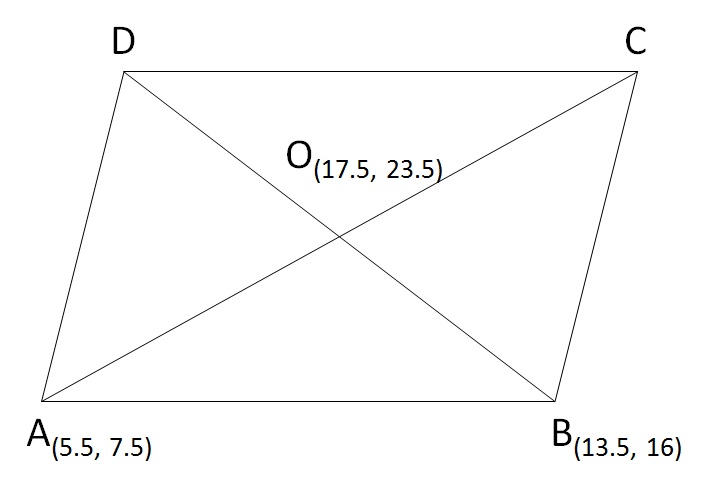
Diagonals of the parallelogram bisect each other.
i.e., they intersect at their mid-points.

From two adjacent vertices of a parallelogram two different diagonals originate.
So, the diagonal from A will be AC and the one from B will be BD.

Because O is the midpoint of AC, the distance AO will be equal to half AC.
Similarly, the distance BO will be equal to half BD.

What is the Approach?

Find OA and OB and double them to get the lengths of the diagonals

The distance between points O(17.5, 23.5) and A(5.5, 7.5)
OA = \\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }\\)
= \\sqrt{ (17.5 - 5.5)^2 + (23.5 - 7.5)^2 }\\) = 20
If OA = 20, AC = 2 * OA = 2 * 20 = 40

Similarly, the distance between points O(17.5, 23.5) and B(13.5, 16)
OB = \\sqrt{ (17.5 - 13.5)^2 + (23.5 - 16)^2 }\\) = 8.5
If OB = 8.5, BD = 2 * OB = 2 * 8.5 = 17.

The lengths of the diagonals are 17 and 40

  The correct answer is Choice D.

Video Explanation