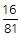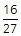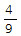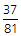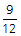Sequences, Series - Progressions: AP, GP & HP

The sequences and series topics includes arithmetic progression (AP), and geometric progression (GP). Occassionally, you may also get questions that test harmonic progression (HP) - likely to find such a question in CAT than in the TANCET. If you are a TANCET aspirant, you could restrict yourself to questions on AP and GP. In addition, you may also find questions on series and sequences that are not part of either of these 3 progressions - likely to find such questions in CAT and GMAT. These aptitude practice questions given below have detailed explanations, and in some cases video explanations. The quantitative reasoning questions have classified on the basis of the concept tested in the question. The level of difficulty of the question is also marked to help you gauge the question.

1. What is the sum of all 3 digit numbers that leave a remainder of '2' when divided by 3?

   1. 897
   2. 1,64,850
   3. 1,64,749
   4. 1,49,700

   Concept: Sum of an AP

   Choice (2)1,64,850 Correct answer Explanatory Answer Medium

2. What is the sum of all positive integers up to 1000, which are divisible by 5 and are not divisible by 2?

   1. 10,050
   2. 5050
   3. 5000
   4. 50,000

   Concept: Sum of AP

   Choice (4)50,000 Correct answer Explanatory Answer Medium

3. The sum of the three numbers in A.P is 21 and the product of the first and third number of the sequence is 45. What are the three numbers?

   1. 5, 7, and 9
   2. 9, 7, and 5
   3. 3, 7, and 11
   4. Both (1) and (2)
   5. None of these

   Concept: 3 numbers in AP

   Choice (4)Both (1) and (2). 5, 7, and 9 or 9, 7, and 5 Correct answer Explanatory Answer Medium

4. A piece of equipment cost a certain factory 600,000. If it depreciates in value, 15% the first year, 13.5 % the next year, 12% the third year, and so on, what will be its value at the end of 10 years, all percentages applying to the original cost?

   1. 2,00,000
   2. 1,05,000
   3. 4,05,000
   4. 6,50,000

   Concept: Sum of AP

   Choice (2) 1,05,000 Correct answer Explanatory Answer Medium

5. The sum of third and ninth term of an A.P is 8. Find the sum of the first 11 terms of the progression.

   1. 44
   2. 22
   3. 19
   4. None of the above

   Concept: Finding term of AP

   Choice (1)44 Correct answer Explanatory Answer Medium

6. Given A = 2⁶⁵ and B = (2⁶⁴+2⁶³+2⁶²+...+2⁰), which of the following is true?

   1. B is 2⁶⁴ larger than A
   2. A and B are equal
   3. B is larger than A by 1
   4. A is larger than B by 1

   Concept: GP Comparison

   Choice (4)A is larger than B by 1 Correct answer Explanatory Answer Medium

7. How many 2-digit positive integers are divisible by 4 or 9?

   1. 32
   2. 22
   3. 30
   4. 34
   5. 10

   Concept: AP - Counting Method

   Choice (3)30 numbers Correct answer Explanatory Answer Medium

8. If a rubber ball consistently bounces back ⅔ of the height from which it is dropped, what fraction of its original height will the ball bounce after being dropped and bounced four times without being stopped?

   1. 
   2. 
   3. 
   4. 
   5. 

   Concept: Decreasing GP

   Choice (1) Correct answer Explanatory Answer Video Explanation TANCET 2013

9. x, 17, 3x - y² - 2 and 3x + y² - 30 are four consecutive terms of an increasing arithmetic sequence. The sum of the four numbers is divisible by:

   1. 2
   2. 3
   3. 5
   4. 7
   5. 11

   Concept: Progression & equations

   Choice (A)The sum is divisible by 2 Correct answer Explanatory Answer Medium XAT 2014

10. What is the sum of the following series?   -64, -66, -68, ..... , -100

    1. -1458
    2. -1558
    3. -1568
    4. -1664
    5. None of the above

    Concept: Sum of an AP

    Choice (B)The sum the sequence is -1558 Correct answer Explanatory Answer Video Solution XAT 2015

11. If log 2, log (2^x -1) and log (2^x + 3) are in A.P, then x is equal to ____

    1. \\frac {5}{2} \\)
    2. log₂5
    3. log₃2
    4. \\frac {3}{2} \\)

    Concept: AP and Logarithm

    Choice (2)The value of x is log₂5 Correct answer Explanatory Answer Hard

12. Two travelers set out on a long odyssey. The first traveler starts from city X and travels north on a certain day and covers 1 km on the first day and on subsequent days, he travels 2 km more than the previous day. After 3 days, a second traveler sets out from city X in the same direction as the first traveler and on his first day he travels 12 km and on subsequent days he travels 1 km more than the previous day. On how many days will the second traveler be ahead of the first?

    1. 2 days
    2. 6 days
    3. From the 2nd day after the 2nd traveler starts
    4. From the 3rd day after the 2nd traveler starts

    Concept: AP and Rates

    Choice (2)The second traveler is ahead of the first for 6 days Correct answer Explanatory Answer Medium