Probability - Practice Questions : Dice
The question given below is a question on finding probabilities of select events when one or more dice are rolled.
Question
What is the probability of getting at least one six in a single throw of three unbiased dice?
(1) 1 / 6
(2) 125 / 216
(3) 1 / 36
(4) 81 / 216
(5) 91 / 216
Correct choice is
(5) and Correct Answer is
91 / 216
Explanatory Answer
Every die has got six sides. Each of the sides is numbered from 1 to 6.
When a single unbiased die is thrown you can have six possible outcomes.
When two dice are thrown simultaneously, the total number of outcomes will be 6 * 6 = 36
Similarly, when three dice are thrown simultaneously, the total number of outcomes will be 6*6*6=216.
We need to find out the number of cases in which at least one of the facing sides shows 6.
At least one means - either one dice or two dice or all three.
Case 1: Let us take the easiest case first - all three dice showing '6' - There is only one such possibility.
Case 2: The number of cases in which two of the dice show 6 and one of them is a different number.
For eg an event like 6 6 5 will be one of the outcomes for case 2.
As two of the dice show '6' , it can happen in only one way. The third die shows a different number, a number other than 6, and it can be any of the 5 other numbers. Therefore, there will 5 possible options i.e. (1, 6, 6), (2, 6, 6), (3, 6, 6), (4, 6, 6), (5, 6, 6).
However, each of these possibilities can have three different arrangements depending upon where the third different digit appears. For example take (1, 6, 6) case - it will have three options (1, 6, 6), (6, 1, 6), (6, 6, 1).
Therefore, the total number of events in which 2 of the dice will show '6' and one will show a different number = 5*3 = 15 cases.
Case 3: When only one of the die shows '6' and the other two show numbers other than '6'.
The die showing '6' has only one option. The other two dice can have any of the '5' options. Therefore, the total number of possibilities = 1*5*5 = 25.
However, the die showing '6' can either be the first die or the second die or the third die.
Therefore, there are a total of 25 * 3 = 75 possibilities.
Total possible outcomes where at least one die shows '6' = Case 1 + Case 2 + Case 3 = 1 + 15 +75 = 91.
Therefore, the required probability =
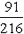Alternate approach:
Find the number of cases in which none of the digits show a '6'.
i.e. all three dice show a number other than '6', 5 * 5 *5 = 125 cases.
Total possible outcomes when three dice are thrown = 216.
The number of outcomes in which at least one die shows a '6' = Total possible outcomes when three dice are thrown - Number of outcomes in which none of them show '6'.
= 216 - 125 = 91.
The required probability =
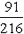
CAT, XAT, TANCET Practice Questions and Answers : Listed Topicwise
Weekend and weekday 
Add to del.icio.us
Stumble It
digg this